오랑우탄의 반란
[ML] 로지스틱회귀 기초 이론 및 수식 정리 (분류 분석) 본문
로지스틱회귀란?
독립변수 Y의 선형 결합을 이용해 사건의 발생 가능성을 예측하는 데 사용되는 통계 기법
로지스틱회귀 이론
만약 X를 연속형 변수로 두고 Y 를 특정 값이 될 확률로 설정한다면, 앞서 배웠던 선형회귀로는 표현이 불가능할 것입니다. 선형 함수는 발산하기 때문에 실제 확률이 0보다 작거나 1보다 크게 나올 수도 있기 때문이지요.
그래서 이 한계를 보완하고자 로지스틱회귀를 사용합니다.
아래 그래프를 보시면 함수에 로그를 취해서 Y값이 0, 1로 수렴하도록 설계된 것을 볼 수 있습니다.
즉, Y가 특정 범주에 속할 때 범주형 변수에 대한 분석으로 로지스틱회귀가 적합합니다.

로지스틱회귀 수식
로그함수가 어떻게 그려지는지 단계별로 살펴보겠습니다.
1. Odds Ratio
Odds ratio (오즈비)란 실패비율 대비 성공비율입니다.
확률 P에 대해 오즈비는 다음과 같이 정의됩니다.

예를 들어 게임을 이길 확률이 80%라고 하면 오즈비는 (80/100) / (20/100) = 4 가 됩니다.
즉 1번 질 때마다 4번은 이긴다는 말로 해석할 수 있지요.
2. Logit
하지만 확률이 클수록 오즈비는 급격히 발산하게 되어 선형회귀함수(y = wx + b)의 y값으로 사용하기 어려워지는데요
이를 해결하고자 오즈비에 로그를 씌워서 확률의 증가에 따라 완만하게 증가하도록 해주고 이를 로짓이라 정의합니다.


로짓을 P에 대해 정리하면 아래의 식이 되어 로짓의 범위는 [−∞,∞] 확률의 범위는 [0,1] 이 됩니다.


로짓을 Y로 두고 선형회귀함수와 합치면 아래의 식이 됩니다.

여기에 지수 e를 취하면 아래의 식이 됩니다.
X값이 w1만큼 증가하면 오즈비는 e^{w1}만큼 증가한다고 해석할 수 있습니다.
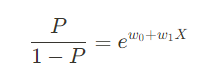
P에 대해 정리한 식에서 로짓에 선형회귀식을 대입하면 아래와 같은 로지스틱회귀 식이 도출됩니다.
즉, w1(가중치) 값을 알면 X 값이 주어졌을 때 해당 사건이 일어날 확률 P 를 알 수 있습니다.
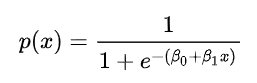
이때, 확률 0.5를 기준으로 0.5 이상이면 사건이 일어남(P(Y) = 1), 0.5 이하면 사건이 일어나지 않음(P(Y) = 0)으로 판단하여 분류 예측에 사용합니다.
분류분석 평가 지표
앞서 회기분석의 평가지표로는 MSE (선형회귀의 경우 r-score까지) 를 사용했는데요,
분류분석의 평가지표로는 정확도와 F1 - Score 를 사용합니다.
실제와 예측값에 대한 모든 경우의 수를 표현한 행렬을 혼동행렬 (confusion matrix) 이라고 합니다.
- 실제와 예측이 같으면 True / 다르면 False
- 예측을 양성으로 했으면 Positive / 음성으로 했으면 Negative
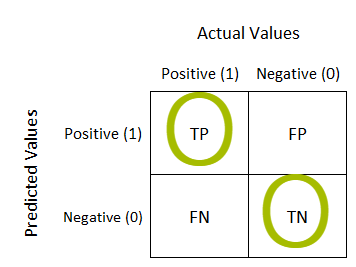
여기서 TP 와 TN 만이 올바르게 분류된 경우입니다.
1. 정밀도 Precision
모델이 양성으로 예측한 결과 (예측 Y) 중 실제 양성의 비율(모델의 관점)
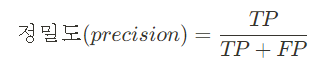
2. 재현율 Recall
실제 값이 양성인 데이터 (실제 Y) 중 모델이 양성으로 예측한 비율 (데이터의 관점)
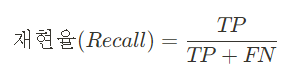
3. F1 - Score
정밀도와 재현율의 조화 평균

4. 정확도 Accuracy
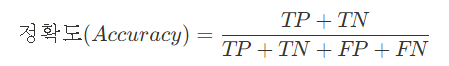
정확도가 제 기능을 못하는 때는 분류에서 특히 Y값이 unbalance하지 못할 때 일어납니다.
따라서 이를 위해서 Y 범주의 비율을 맞춰주거나 평가 지표를 f1 - score을 사용함으로써 이를 보완합니다.
선형회귀 vs 로지스틱회귀
| 선형회귀 (회귀) Linear Regression |
로지스틱회귀 (분류) Logistic Regression |
|
| 모델 생성이 쉬움 가중치/회귀계수를 통한 해석이 쉬움 X변수에 범주형, 수치형 변수 둘 다 사용 가능 |
||
| 종속변수 Y | 수치형 | 범주형 |
| 평가척도 | MSE, R Square (선형회귀만) | Accuracy, F1-score |
| 모델 클래스 | sklearn.linear_model.LinearRegression | sklearn.linear_model.LogisticRegression |
| 평가 클래스 | sklearn.metrics.mean_squared_error sklearn.metrics.r2_score |
sklearn.metrics.accuracy_score sklearn.metrics.f1_score |
'PYTHON > 머신러닝' 카테고리의 다른 글
| [ML] 데이터분석 예측모델링 파이썬 실습 (타이타닉) (0) | 2024.08.13 |
|---|---|
| [ML] (다중)로지스틱회귀 분류 분석 파이썬 실습 (VSCode) (0) | 2024.08.12 |
| [ML] 머신러닝 다중선형회귀분석 파이썬 실습 (VSCode) (0) | 2024.08.09 |
| [ML] 머신러닝 선형회귀분석 파이썬 실습 (VSCode) (0) | 2024.08.09 |
| [ML] 선형회귀 기초 이론 및 수식 정리 (회귀 분석) (0) | 2024.08.08 |